This is all about endianness. That is, how the bits are arranged in memory. You can arrange these bits in memory 2 ways. In big endian or in little endian. Go to wikipedia for some background but esssentially big endian is the way the decimal system works and little endian is the reverse of this.
Big Endian: One hundred and twenty three is stored as 123.
Ie the most significant figure (MSF) is on the left.
Little Endian: One hundred and twenty three is stored as 321.
Ie the MSF is on the right.
be32enc and le32enc are cool functions that transform an input into either big or little endian.
Let’s look at an example.
Here is the code:
#include <stdio.h>
#include <stdlib.h>
static inline void be32enc(void *pp, uint32_t x)
{
uint8_t *p = (uint8_t *)pp;
p[3] = x & 0xff;
p[2] = (x >> 8) & 0xff;
p[1] = (x >> 16) & 0xff;
p[0] = (x >> 24) & 0xff;
}
static inline void le32enc(void *pp, uint32_t x)
{
uint8_t *p = (uint8_t *)pp;
p[0] = x & 0xff;
p[1] = (x >> 8) & 0xff;
p[2] = (x >> 16) & 0xff;
p[3] = (x >> 24) & 0xff;
}
int main(int argc, char const *argv[])
{
unsigned char *input;
input = malloc(32);
be32enc((uint32_t *)input,0xffff); /* version */
return 0;
}
Here we are calling the be32enc function and passing in 0xffff which is 65535 in decimal.
The be32enc function takes a pointer to the input and the data that we want to store (0xffff) and goes to work. The input is nothing more than 32 bits in memory. If you were to print the input variable, it would be 32 zeros. (Technical note: This is not always the case because we didn’t actually initialise it and because it’s a pointer, it points to the memory address of the first element anyway).
The pointer pp to the input is then cast from an unsigned 32 bit integer to an unsigned 8 bit integer. This is a neat trick to allow the 0xff mask to operate on 8 bits at a time.
p[3] = x & 0xff;
The data (x) which is 65535 is then masked with 0xff. The effect of this is that it preserves the first 8 bits when counting from right to left.
11111111 11111111 (x)
00000000 11111111 (& 0xff)
————————
00000000 11111111
The result is then placed in p[3]. This is important because if you look at the le32enc function, the ordering is reversed and the result is placed in p[0] instead.
Next we have
p[2] = (x >> 8) & 0xff;
which means shift x 8 bits to the right and mask again and put the result in p[2]
11111111 11111111 (x)
00000000 11111111 (& 0xff)
————————
00000000 11111111
For p[2] and p[1], the output will be all zero’s.
00000000 00000000 (x)
00000000 11111111 (& 0xff)
————————
00000000 00000000
After all of this, the input becomes
11111111 11111111 00000000 00000000
….p[3]…….. p[2]…….. p[1]…….. p[0]
If you were to print this in decimal in a debugger you would get 4294901760
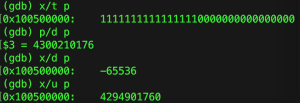
To interprete the image above:
x/t p: display the memory location of p in binary.
p/d p: display the value of the pointer address in decimal. (This can be ignored).
x/d p: display the value in memory location of p in decimal.
x/u p: display the value of memory location of p as an unsigned decimal.
What has happened here? I’ve taken 0xffff or 65535 and put it in big endian format which has resulted in 4294901760. I’m showing the decimal because it is often easier to digest that hex or binary.
If I was to run the le32enc, you would get no change. The output would be 65535.
Summary
The reason why this is important to understand is that in certain protocols (bitcoins) or certain hardware, it is important to know how the data is arranged. Sometimes it is big endian and sometimes it is little endian. It maybe frustrating to try and figure it out, but hopefully this article will shed some light on how it works under the covers.